Machine learning algorithms for intrusion detection

This section will cover ML methods such as clustering, autoencoders, SVM, and isolation forests, which can be used for anomaly detection.

Density-based scan (DBSCAN)

In the previous chapter where we introduced unsupervised ML (UML), we studied the concept of clustering via the K-Means clustering algorithm. However, recall that K is a hyperparameter that has to be set manually; there is no good way to know the ideal number of clusters in advance. DBSCAN is a density-based clustering algorithm that does not need a pre-specified number of clusters.

DBSCAN hinges on two parameters: the minimum number of points required to call a group of points a cluster and ξ (which specifies the minimum distance between two points to call them neighbors). Internally, the algorithm classifies every data point as being from one of the following three categories:

• Core points are those that have at least the minimum number of points in the neighborhood defined by a circle of radius ξ
• Border points, which are not core points, but in the neighborhood area or cluster of a core point described previously
• An anomaly point, which is neither a core point nor reachable from one (that is, not a border point either)

In a nutshell, the process works as follows:

1. Set the values for the parameters, the minimum number of points, and ξ.
2. Choose a starting point (say, A) at random, and find all points at a distance of ξ or less from this point.
3. If the number of points meets the threshold for the minimum number of points, then A is a core point, and a cluster can form around it. All the points at a distance of ξ or less are border points and are added to the cluster centered on A.
4. Repeat these steps for each point. If a point (say, B) added to a cluster also turns out to be a core point, we first form its own cluster and then merge it with the original cluster around A.

Thus, DBSCAN is able to identify high-density regions in the feature space and group points into clusters. A point that does not fall within a cluster is determined to be anomalous or an outlier. DBSCAN offers two powerful advantages over the K-Means clustering discussed earlier:

• We do not need to specify the number of clusters. Oftentimes, when analyzing data, and especially in unsupervised settings, we may not be aware of the number of classes in the data. We, therefore, do not know what the number of clusters should be for anomaly detection. DBSCAN eliminates this problem and forms clusters appropriately based on density.
• DBSCAN is able to find clusters that have arbitrary shapes. Because it is based on the density of regions around the core points, the shape of the clusters need not be circular. K-Means clustering, on the other hand, cannot detect overlapping or arbitrary-shaped clusters.

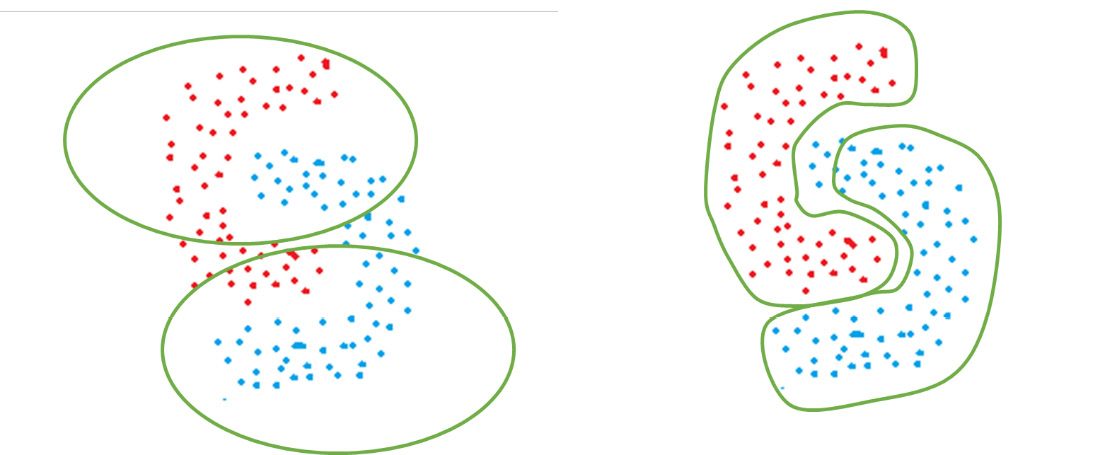
As an example of the arbitrary shape clusters that DBSCAN forms, consider the following figure. The color of the points represents the ground-truth labels of the classes they belong to. If K-Means is used, circularly shaped clusters are formed that do not separate the two classes. On the other hand, if we use DBSCAN, it is able to properly identify clusters based on density and separate the two classes in a much better manner:

Figure 2.13 – How K-Means (left) and DBSCAN (right) would perform for irregularly shaped clusters

The Python implementation of DBSCAN is as follows:

from sklearn.neighbors import DBSCAN
actual_labels = data4["Label"]
X = data4.drop(["Label", "target","protocol_type", "service","flag"], axis=1)
epsilon = 0.2
minimum_samples = 5
clf = DBSCAN( eps = epsilon,  min_samples = minimum_samples)
predicted_labels = clf.fit_predict(X)

After rescoring the labels, we can plot the confusion matrix. You should see something like this:

Figure 2.14 – Confusion matrix for DBSCAN

This presents an interesting confusion matrix. We see that all of the outliers are being detected—but along with it, a large number of inliers are also being wrongly classified as outliers. This is a classic case of low precision and high recall.

We can experiment with how this model performs as we vary its two parameters. For example, if we run the same block of code with minimum_samples = 1000 and epsilon = 0.8, we will get the following confusion matrix:

Figure 2.15 – Confusion matrix for DBSCAN

This model is worse than the previous one and is an extreme case of low precision and high recall. Everything is predicted to be an outlier.

What happens if you set epsilon to a high value—say, 35? You end up with the following confusion matrix:

Figure 2.16 – Confusion matrix for improved DBSCAN

Somewhat better than before! You can experiment with other values of the parameters to find out what works best.

One-class SVM

Support vector machine (SVM) is an algorithm widely used for classification tasks. One-class SVM (OC-SVM) is the version used for anomaly detection. However, before we turn to OC-SVM, it would be helpful to have a primer into what SVM is and how it actually works.

Support vector machines

The fundamental goal of SVM is to calculate the optimal decision boundary between two classes, also known as the separating hyperplane. Data points are classified into a category depending on which side of the hyperplane or decision boundary they fall on.

For example, if we consider points in two dimensions, the orange and yellow lines as shown in the following figure are possible hyperplanes. Note that the visualization here is straightforward because we have only two dimensions. For 3D data, the decision boundary will be a plane. For n-dimensional data, the decision boundary will be an n-1-dimensional hyperplane:

Figure 2.17 – OC-SVM

We can see that in Figure 2.17, both the orange and yellow lines are possible hyperplanes. But how does the SVM choose the best hyperplane? It evaluates all possible hyperplanes for the following criteria:

• How well does this hyperplane separate the two classes?
• What is the smallest distance between data points (on either side) and the hyperplane?

Ideally, we want a hyperplane that best separates the two classes and has the largest distance to the data points in either class.

In some cases, points may not be linearly separable. SVM employs the kernel trick; using a kernel function, the points are projected to a higher-dimension space. Because of the complex transformations, points that are not linearly separable in their original low-dimensional space may become separable in a higher-dimensional space. Figure 2.18 (drawn from https://sebastianraschka.com/faq/docs/select_svm_kernels.html) shows an example of a kernel transformation. In the original two-dimensional space, the classes are not linearly separable by a hyperplane. However, when projected into three dimensions, they become linearly separable. The hyperplane calculated in three dimensions is mapped back to the two-dimensional space in order to make predictions:

Figure 2.18 – Kernel transformations

SVMs are effective in high-dimensional feature spaces and are also memory efficient since they use a small number of points for training.

The OC-SVM algorithm

Now that we have a sufficient background into what SVM is and how it works, let us discuss OC-SVM and how it can be used for anomaly detection.

OC-SVM has its foundations in the concepts of Support Vector Data Description (also known as SVDD). While SVM takes a planar approach, the goal in SVDD is to build a hypersphere enclosing the data points. Note that as this is anomaly detection, we have no labels. We construct the hypersphere and optimize it to be as small as possible. The hypothesis behind this is that outliers will be removed from the regular points, and will hence fall outside the spherical boundary.

For every point, we calculate the distance to the center of the sphere. If the distance is less than the radius, the point falls inside the sphere and is benign. If it is greater, the point falls outside the sphere and is hence classified as an anomaly.

The OC-SVM algorithm can be implemented in Python as follows:

from sklearn import svm
actual_labels = data4["Label"]
X = data4.drop(["Label", "target","protocol_type", "service","flag"], axis=1)
clf = svm.OneClassSVM(kernel="rbf")
clf.fit(X)
predicted_labels = clf.predict(X)

Plotting the confusion matrix, this is what we see:

Figure 2.19 – Confusion matrix for OC-SVM

Okay—this seems to be an improvement. While our true positives have decreased, so have our false positives—and by a lot.

Isolation forest

In order to understand what an isolation forest is, it is necessary to have an overview of decision trees and random forests.

Decision trees

A decision tree is an ML algorithm that creates a hierarchy of rules in order to classify a data point. The leaf nodes of a tree represent the labels for classification. All internal nodes (non-leaf) represent rules. For every possible result of the rule, a different child is defined. Rules are such that outputs are generally binary in nature. For continuous features, the rule compares the feature with some value. For example, in our fraud detection decision tree, Amount > 10,000 is a rule that has outputs as 1 (yes) or 0 (no). In the case of categorical variables, there is no ordering, and so a greater-than or less-than comparison is meaningless. Rules for categorical features check for membership in sets. For example, if there is a rule involving the day of the week, it can check whether the transaction fell on a weekend using the Day € {Sat, Sun} rule.

The tree defines the set of rules to be used for classification; we start at the root node and traverse the tree depending on the output of our rules.

A random forest is a collection of multiple decision trees, each trained on a different subset of data and hence having a different structure and different rules. While making a prediction for a data point, we run the rules in each tree independently and choose the predicted label by a majority vote.

The isolation forest algorithm

Now that we have set a fair bit of background on random forests, let us turn to isolation forests. An isolation forest is an unsupervised anomaly detection algorithm. It is based on the underlying definition of anomalies; anomalies are rare occurrences and deviate significantly from normal data points. Because of this, if we process the data in a tree-like structure (similar to what we do for decision trees), the non-anomalous points will require more and more rules (which means traversing more deeply into the tree) to be classified, as they are all similar to each other. Anomalies can be detected based on the path length a data point takes from the root of the tree.

First, we construct a set of isolation trees similar to decision trees, as follows:

1. Perform a random sampling over the data to obtain a subset to be used for training an isolation tree.
2. Select a feature from the set of features available.
3. Select a random threshold for the feature (if it is continuous), or a random membership test (if it is categorical).
4. Based on the rule created in step 3, data points will be assigned to either the left branch or the right branch of the tree.
5. Repeat steps 2-4 recursively until each data point is isolated (in a leaf node by itself).

After the isolation trees have been constructed, we have a trained isolation forest. In order to run inferencing, we use an ensemble approach to examine the path length required to isolate a particular point. Points that can be isolated with the fewest number of rules (that is, closer to the root node) are more likely to be anomalies. If we have n training data points, the anomaly score for a point x is calculated as follows:

s(x, n) = 2 − E(h(x)) _ c(n) 

Here, h(x) represents the path length (number of edges of the tree traversed until the point x is isolated). E(h(x)), therefore, represents the expected value or mean of all the path lengths across multiple trees in the isolation forest. The constant c(n) is the average path length of an unsuccessful search in a binary search tree; we use it to normalize the expected value of h(x). It is dependent on the number of training examples and can be calculated using the harmonic number H(n) as follows:

c(n) = 2H(n − 1) − 2(n − 1) / n

The value of s(x, n) is used to determine whether the point x is anomalous or not. Higher values closer to 1 indicate that the points are anomalies, and smaller values indicate that they are normal.

The scikit-learn package provides us with an efficient implementation for an isolation forest so that we don’t have to do any of the hard work ourselves. We simply fit a model and use it to make predictions. For simplicity of our analysis, let us use only the continuous-valued variables, and ignore the categorical string variables for now.

First, we will use the original DataFrame we constructed and select the columns of interest to us. Note that we must record the labels in a list beforehand since labels cannot be used during model training. We then fit an isolation forest model on our features and use it to make predictions:

from sklearn.ensemble import IsolationForest
actual_labels = data["Label"]
X = data.drop(["Label", "target","protocol_type", "service","flag"], axis=1)
clf = IsolationForest(random_state=0).fit(X)
predicted_labels = clf.predict(X)

The predict function here calculates the anomaly score and returns a prediction based on that score. A prediction of -1 indicates that the example is determined to be anomalous, and that of 1 indicates that it is not. Recall that our actual labels are in the form of 0 and 1, not -1 and 1. For an apples-to-apples comparison, we will recode the predicted labels, replacing 1 with 0 and -1 with 1:

predicted_labels_rescored =
[1 if pred == -1 else 0 for pred in predicted_labels]

Now, we can plot a confusion matrix using the actual and predicted labels, in the same way that we did before. On doing so, you should end up with the following plot:

Figure 2.20 – Confusion matrix for isolation forest

We see that while this model predicts the majority of benign classes correctly, it also has a significant chunk of false positives and negatives.

Autoencoders

Autoencoders (AEs) are deep neural networks (DNNs) that can be used for anomaly detection. As this is not an introductory book, we expect you to have some background and a preliminary understanding of deep learning (DL) and how neural networks work. As a refresher, we will present some basic concepts here. This is not meant to be an exhaustive tutorial on neural networks.

A primer on neural networks

Let us now go through a few basics of neural networks, how they are formed, and how they work.

Neural networks – structure

The fundamental building block of a neural network is a neuron. This is a computational unit that takes in multiple numeric inputs and applies a mathematical transformation on it to produce an output. Each input to a neuron has a weight associated with it. The neuron first calculates a weighted sum of the inputs and then applies an activation function that transforms this sum into an output. Weights represent the parameters of our neural network; training a model means essentially finding the optimum values of the weights such that the classification error is reduced.

A sample neuron is depicted in Figure 2.21. It can be generalized to a neuron with any number of inputs, each having its own weight. Here, σ represents the activation function. This determines how the weighted sum of inputs is transformed into an output:

Figure 2.21 – Basic structure of a neuron

A group of neurons together form a layer of neurons, and multiple such layers connected together form a neural network. The more the number of layers, the deeper the network is said to be. Input data (in the form of features) is fed to the first layer. In the simplest form of neural networks, every neuron in a layer is connected to every neuron in the next layer; this is known as a fully connected neural network (FCNN).

The final layer is the output layer. In the case of binary classification, the output layer has only one neuron with a sigmoid activation function. The output of this neuron indicates the probability of the data point belonging to the positive class. If it is a multiclass classification problem, then the final layer contains as many neurons as the number of classes, each with a softmax activation. The outputs are normalized such that each one represents the probability of the input belonging to a particular class, and they all add up to 1. All of the layers other than the input and output are not visible from the outside; they are known as hidden layers.

Putting all of this together, Figure 2.22 shows the structure of a neural network:

Figure 2.22 – A neural network

Let us take a quick look at four commonly used activation functions: sigmoid, tanh, rectified linear unit (ReLU), and softmax.

Neural networks – activation functions

The sigmoid function normalizes a real-valued input into a value between 0 and 1. It is defined as follows:

f(z) =  1 _ 1+ e −z 

If we plot the function, we end up with a graph as follows:

Figure 2.23 – sigmoid activation

As we can see, any number is squashed into a range from 0 to 1, which makes the sigmoid function an ideal candidate for outputting probabilities.

The hyperbolic tangent function, also known as the tanh function, is defined as follows:

tanh(z) =  2 _ 1+ e −2z  − 1

Plotting this function, we see a graph as follows:

Figure 2.24 – tanh activation

This looks very similar to the sigmoid graph, but note the subtle differences: here, the output of the function ranges from -1 to 1 instead of 0 to 1. Negative numbers get mapped to negative values, and positive numbers get mapped to positive values. As the function is centered on 0 (as opposed to sigmoid centered on 0.5), it provides better mathematical conveniences. Generally, we use tanh as an activation function for hidden layers and sigmoid for the output layer.

The ReLU activation function is defined as follows:

ReLU (z) = {max(0, z); z ≥ 0 0 ; z < 0 

Basically, the output is the same as the input if it is positive; else, it is 0. The graph looks like this:

Figure 2.25 – ReLU activation

The softmax function can be considered to be a normalized version of sigmoid. While sigmoid operates on a single input, softmax will operate on a vector of inputs and produce a vector as output. Each value in the output vector will be between 0 and 1. If the vector Z is defined as [z1, z2, z3 ….. zK], softmax is defined as follows:

σ (z i) =  e z i _ ∑ j=1 j=K e z j 

Basically, we first calculate the sigmoid values for each element in the vector and form a sigmoid vector. Then, we normalize this vector by the total so that each element is between 0 and 1 and they add up to 1 (representing probabilities). This can be better illustrated with a concrete example.

Say that our output vector Z has three elements: Z = [2, 0.9, 0.1]. Then, we have z1= 2, z2 = 0.9, and z3 = 0.1; we therefore have e z 1 = e 2 = 7.3890, e z 2 = e 0.9 = 2.4596, and e z 3 = e 0.1 = 1.1051. Applying the previous equation, the denominator is the sum of these three, which is 10.9537. Now, the output vector is simply the ratio of each element to this summed-up value—that is, [ 7.3890 _ 10.9537,  2.4596 _ 10.9537,  1.1051 _ 10.9537], which comes out to be [0.6745, 0.2245, 0.1008]. These values represent probabilities of the input belonging to each class respectively (they do not add up to 1 because of rounding errors).

Now that we have an understanding of activation functions, let us discuss how a neural network actually functions from end to end.

Neural networks – operation

When a data point is passed through a neural network, it undergoes a series of transformations through the neurons in each layer. This phase is known as the forward pass. As the weights are assigned randomly at the beginning, the output at each neuron is different. The final layer will give us the probability of the point belonging to a particular class; we compare this with our ground-truth labels (0 or 1) and calculate a loss. Just as mean squared error (MSE) in linear regression is a loss function indicating the error, classification in neural networks uses binary cross-entropy and categorical cross-entropy as the loss for binary and multiclass classification respectively.

Once the loss is calculated, it is passed back through the network in a process called backpropagation. Every weight parameter is adjusted based on how it contributes to the loss. This phase is known as the backward pass. The same gradient descent that we learned before applies here too! Once all the data points have been passed through the network once, we say that a training epoch has completed. We continue this process multiple times, with the weights changing and the loss (hopefully) decreasing in each iteration. The training can be stopped either after a fixed number of epochs or if we reach a point where the loss changes only minimally.

Autoencoders – a special class of neural networks

While a standard neural network aims to learn a decision function that will predict the class of an input data point (that is, classification), the goal of autoencoders is to simply reconstruct a data point. While training autoencoders, both the input and output that we provide to the autoencoder are the same, which is the feature vector of the data point. The rationale behind it is that because we train only on normal (non-anomalous) data, the neural network will learn how to reconstruct it. On the anomalous data, however, we expect it to fail; remember—the model was never exposed to these data points, and we expect them to be significantly different than the normal ones. As a result, the error in reconstruction is expected to be high for anomalous data points, and we use this error as a metric to determine whether a point is an anomaly.

An autoencoder has two components: an encoder and a decoder. The encoder takes in input data and reduces it to a lower-dimensional space. The output of the encoder can be considered to be a dimensionally reduced version of the input. This output is fed to the decoder, which then projects it into a higher-dimensional subspace (similar to that of the input).

Here is what an autoencoder looks like:

Figure 2.26 – Autoencoder

We will implement this in Python using a framework known as keras. This is a library built on top of the TensorFlow framework that allows us to easily and intuitively design, build, and customize neural network models.

First, we import the necessary libraries and divide our data into training and test sets. Note that while we train the autoencoder only on normal or non-anomalous data, in the real world it is impossible to have a dataset that is 100% clean; there will be some contamination involved. To simulate this, we train on both the normal and abnormal examples, with the abnormal ones being very small in proportion. The stratify parameter ensures that the training and testing data has a similar distribution of labels so as to avoid an imbalanced dataset. The code is illustrated in the following snippet:

from tensorflow import keras
from tensorflow.keras import layers
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X,
                        actual_labels,
                        test_size=0.33,
                        random_state=42,
                        stratify=actual_labels)
X_train = np.array(X_train, dtype=np.float)
X_test = np.array(X_test, dtype=np.float)

We then build our neural network using keras. For each layer, we specify the number of neurons. If our feature vector has N dimensions, the input layer would have to have N layers. Similarly, because this is an autoencoder, the output layer would also have N layers.

We first build the encoder part. We start with an input layer, followed by three fully connected layers of decreasing dimensions. To each layer, we feed the output of the previous layer as input:

input = keras.Input(shape=(X_train.shape[1],))
encoded = layers.Dense(30, activation='relu')(input)
encoded = layers.Dense(16, activation='relu')(encoded)
encoded = layers.Dense(8, activation='relu')(encoded)

Now, we work our way back to higher dimensions and build the decoder part:

decoded = layers.Dense(16, activation='relu')(encoded)
decoded = layers.Dense(30, activation='relu')(decoded)
decoded = layers.Dense(X_train.shape[1], activation='sigmoid')(encoded)

Now, we put it all together to form the autoencoder:

autoencoder = keras.Model(input, decoded)

We also define the encoder and decoder models separately, to make predictions later:

# Encoder
encoder = keras.Model(input_img, encoded)
# Decoder
encoded_input = keras.Input(shape=(encoding_dim,))
decoder_layer = autoencoder.layers[-1]
decoder = keras.Model(encoded_input,decoder_layer(encoded_input))

If we want to examine the structure of the autoencoder, we can compile it and print out a summary of the model:

autoencoder.compile(optimizer='adam', loss='mse')
autoencoder.summary()

You should see which layers are in the network and what their dimensions are as well:

Figure 2.27 – Autoencoder model summary

Finally, we actually train the model. Normally, we provide features and the ground truth for training, but in this case, our input and output are the same:

autoencoder.fit(X_train, X_train,
                epochs=10,
                batch_size=256,
                shuffle=True)

Let’s see the result:

Figure 2.28 – Training phase

Now that the model is fit, we can use it to make predictions. To evaluate this model, we will predict the output for each input data point, and calculate the reconstruction error:

from sklearn.metrics import mean_squared_error
predicted = autoencoder.predict(X_test)
errors = [np.linalg.norm(X_test[idx] - k[idx]) for idx in range(X_test.shape[0])]

Now, we need to set a threshold for the reconstruction error, after which we will call data points as anomalies. The easiest way to do this is to leverage the distribution of the reconstruction error. Here, we say that when the error is above the 99th percentile, it represents an anomaly:

thresh = np.percentile(errors, 99)
predicted_labels = [1 if errors[idx] > thresh else 0 for idx in range(X_test.shape[0])]

When we generate the confusion matrix, we see something like this:

Figure 2.29 – Confusion matrix for Autoencoder

As we can see, this model is a very poor one; there are absolutely no true positives here.