Higher order functions

Unix shells allow us to express computations as pipelines. Small programs called filters are piped together in unforeseen ways to ensure they work together. For example, refer to this code:

~> seq 100 | paste -s -d '*' | bc

This is a very big number (obviously, as we just generated numbers from 1 to 100 and multiplied them together). There is looping involved, of course. We need to generate numbers from 1 to 100, connect them together via paste, and pass these on to bc. Now consider the following code:

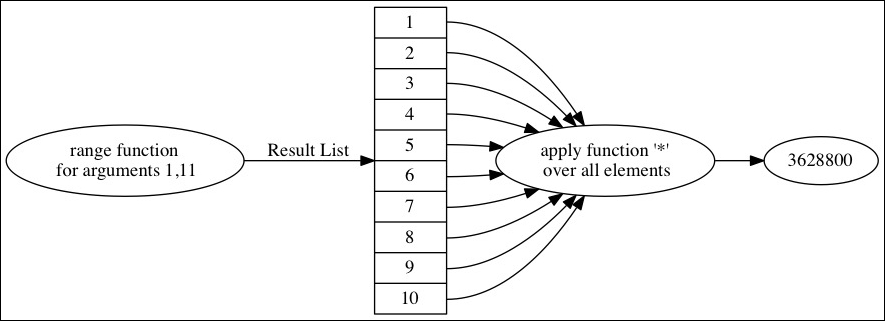
scala> val x = (1 to 10).toList 
x: List[Int] = List(1, 2, 3, 4, 5, 6, 7, 8, 9, 10) 
 
scala> x.foldLeft(1) { (r,c) => r * c } 
res2: Int = 3628800

Writing a for loop with a counter and iterating over the elements of the collection one by one is shown in the preceding code. We simply don't have to worry about visiting all the elements now. Instead, we start thinking of how we can process each element.

Here is the equivalent Clojure code:

user=> (apply * (range 1 11) ) 
3628800

The following figure shows how the code works:

Scala's foldLeft and Clojure's apply are higher order functions. They help us avoid writing boilerplate code. The ability to supply a function brings a lot of flexibility to the table.

Eschewing null checks

Higher order functions help us succinctly express logic. There is an alternative paradigm that expresses logic without resorting to null checks. Refer to http://www.infoq.com/presentations/Null-References-The-Billion-Dollar-Mistake-Tony-Hoare on why nulls are a bad idea; it comes directly from its inventor.

Here is a Scala collection with some strings and numbers thrown in; it is written using the alternative paradigm:

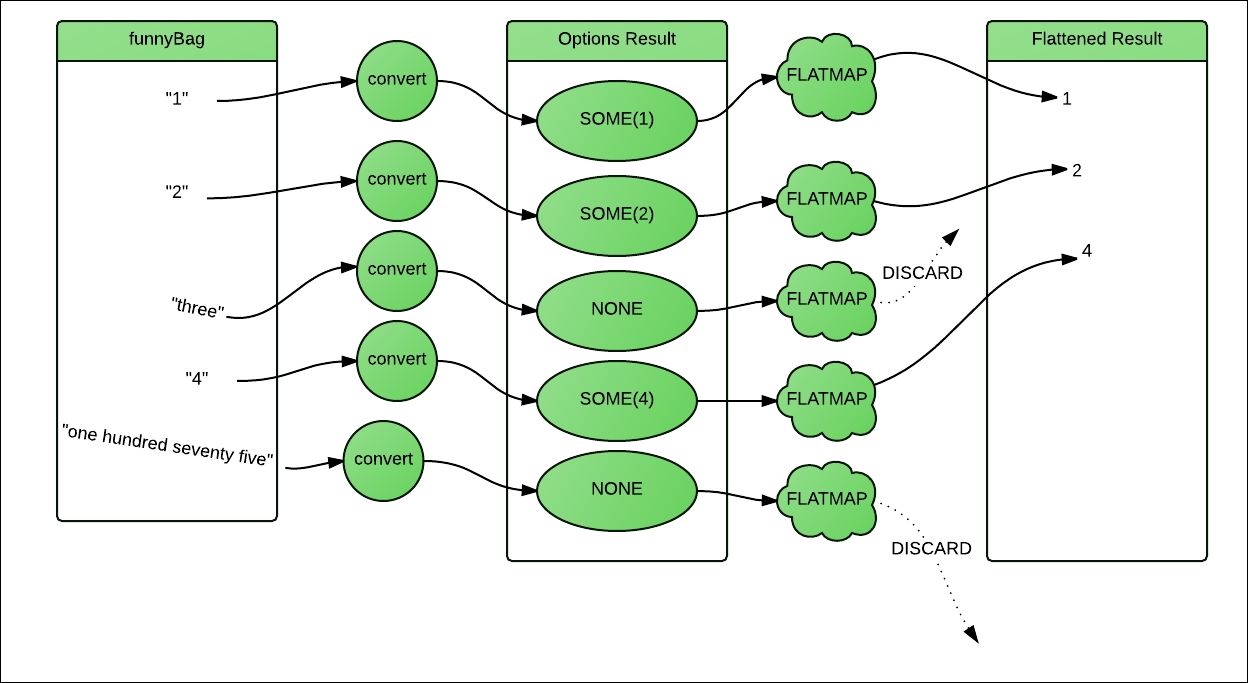
scala> val funnyBag = List("1", "2", "three", "4", "one hundred seventy five") 
funnyBag: List[String] = List(1, 2, three, 4, one hundred seventy five)

We want to extract the numbers out of this collection and sum them up:

scala> def toInt(in: String): Option[Int] = { 
     |   try { 
     |     Some(Integer.parseInt(in.trim)) 
     |   } catch { 
     |       case e: Exception => None 
     |   } 
     | } 
toInt: (in: String)Option[Int]

We return an Option container as a return value. If the string was successfully parsed as a number, we return Some[Int], holding the converted number.

The following diagram shows the execution flow:

In the case of a failure, we return None. Now the following higher order function skips None and just flattens Some. The flattening operation pulls out the result value out of Some:

scala> funnyBag.flatMap(toInt) 
res1: List[Int] = List(1, 2, 4)

We can now do further processing on the resulting number list, for example, summing it up:

scala> funnyBag.flatMap(toInt).sum 
res2: Int = 7

Learning Functional Data Structures and Algorithms

By : S. Khot, Mishra

Learning Functional Data Structures and Algorithms

By: S. Khot, Mishra

Overview of this book

Higher order functions

Eschewing null checks

Learning Functional Data Structures and Algorithms

By : S. Khot, Mishra

Learning Functional Data Structures and Algorithms

By: S. Khot, Mishra

Overview of this book

Higher order functions

Eschewing null checks

Create a Note

Delete Bookmark

Delete Note

Edit Note

Confirmation

Buy this book with your credits?