Computing paradigms can be defined as the significant milestones that have been achieved over the years. To say that computers have made the lives of humans easier is an understatement. On a daily basis, we need machines that can analyze, simulate, and optimize solutions to complex problems. Although the shapes and sizes of computers have changed over time, they still operate on the doctrines proposed by Alan Turing and John von Neumann.
In this section, we will study the evolution of quantum technology over the years. We will also study some of the technology’s limitations in the face of certain business challenges.
The evolution of computing paradigms
Turing showed us the types of problems computers can solve, von Neumann built programmable computers, and Michael Moore’s pioneering work in semiconductors made computers more capable. Figure 1.1 shows the advancement of computing paradigms over the years, and their ability to affect growth in human history:
|
1821
|
Mechanical calculator
|
Has Enabled humans to migrate from mechanical devices to electronic devices with better accuracy in calculations.
|
|
1890
|
Punch-card system
|
Demonstrated first use case of large-scale computing by aiding in the US Census.
|
|
1936
|
Turing machine
|
Theoretical conceptual framework was laid down to solve large computational problems.
|
|
1941
|
Digital electronic computer
|
First time a computer was able to store information on its main memory.
|
|
1945
|
Electronic Numerical Integrator and Calculator (ENIAC)
|
First digital computer to perform large class of numerical problems through reprogramming.
|
|
1958
|
Integrated Circuit (IC)
|
Helped in the transition of enterprise-level computing to personal computing.
|
|
1976
|
Cray-1 Supercomputer
|
Aided 240 million calculations useful for large-scale scientific applications and simulations.
|
|
1997
|
Parallel computing
|
Multiple-CPU core was used to solve complex problems in a limited timeframe, enabling Google to form a better search engine.
|
|
2006
|
Cloud computing
|
Technology has enabled users to access large computational resources from remote locations.
|
|
2016
|
Reprogrammable quantum computer
|
Offers a better platform to solve complex simulation or optimization problems in comparison to classical computers
|
|
2017
|
Molecular informatics
|
Harnesses molecular properties for rapid, scalable information storage and processing.
|
Figure 1.1 – Evolution of computing paradigms
The evolution of computing technology has enabled humans to evolve from an agrarian society to an industrial society. Progress in computing prowess has catapulted society from bartering goods to building e-commerce platforms. Figure 1.1 has given a conclusive summary of how computing technology has benefitted society through its progression from a device that merely performs calculations to the multifunction device in its present form. In the next section, we are going to assess the challenges faced by large-scale businesses and the limitations of current digital technology in addressing them.
Business challenges and technology solutions
Current digital technologies have advantages as well as limitations in providing solutions and insights in real time. The rise of numerous variables and their increasing complexity can affect decision-making in the real world. It is essential to have technology that is reliable and accurate, and fast-paced at the same time. The need for a reliable technology stack has prompted scientists worldwide to investigate technology that is beyond the reach of humans. The current challenges faced by large-scale businesses are as follows:
- Faster task completion: In the current era, where manufacturing firms are looking to achieve super-large-scale production capacity and efficiency, there is a need to build faster and more reliable systems. For instance, according to an exciting study by Artificial Brain (How Artificial Brain is Building an Optimal Algorithm for EV Charger Placement Using Quantum Annealing and a Genetic Algorithm, Quantum Zeitgeist, https://tinyurl.com/bdep5eze) regarding setting up charging stations within a 50-mile radius in the San Francisco Bay Area, around 8,543,811,434,435,330 combinations were possible. Now, how can this distribution be optimized when such a large number of combinations is possible? A quantum computer theoretically solved this problem in less than 3 seconds.
- Content discovery: With the advent of social media websites, a plethora of content is available to analyze. This content is available in different sizes and shapes, in the form of text and images. An organization would need a computer with superior computing power to explore this content. This special computing prowess was achieved through parallel computing and local optimization of the machines. However, much needs to be achieved in this field in order to mine real-time business insights from the underlying data. Quantum natural language processing (QNLP) is a promising technique to resolve problems in real time.
- Lower administration costs: It is always a good strategy to optimize costs. Automation of mega factories has provided the owners with a solution in the right direction. Large-scale automation comes with a set of problems of its own, but precision and real-time decision-making help to make it more accurate and reliable. Recently, BMW has come up with a challenge where competitors have to focus on solving problems based on pre-production vehicle configuration, material deformation in production, vehicle sensor placement, and machine learning for automated quality assessment. Based on the results obtained, Dr. Peter Lehnert, BMW Group’s Vice President of Research and New Technologies Digital Car, commented: “We at the BMW Group are convinced that future technologies such as quantum computing have the potential to make our products more desirable and sustainable” (Winners announced in the BMW Group Quantum Computing Challenge, AWS Quantum Computing Blog, https://aws.amazon.com/blogs/quantum-computing/winners-announced-in-the-bmw-group-quantum-computing-challenge/).
- Remote working: The year 2020 played a pivotal role in the history of humankind. Due to the advent of COVID-19, humans have discovered that they can work from anywhere in the world. This has given rise to the demand for remote working from management and employees. Since there are some instances where you need higher computing power, remote working might not be feasible at all times. However, with most technologies going online and providing a real-time experience of working in the office environment through virtual and augmented reality and better connectivity, businesses can overcome this particular challenge. At the same time, it lowers the administration costs for management. It also helps in reducing storage costs further, which helps in reducing the unit cost for the company.
In order to perform a business task more efficiently and optimally, the business fraternity has started looking for technological solutions. Digital computing in its current state has helped businesses to achieve more efficiency via automation and augmented intelligence. However, current hardware technology has not been able to solve a few complex tasks, which can be associated with an abundance of data and the limitation of computing memory. The following section highlights the types of problems that can be solved by digital computing, and other problems that have generated the need to look beyond the current computing paradigm.
Current business challenges and limitations of digital technology
Digital computers are powered by integrated circuits (ICs), a technology that reached its peak in the 20th century. According to Moore’s law, the number of transistors powering microchips will double every year. In 2021, IBM announced that it can fit 50 billion transistors into its 2 nm chip technology, which basically allows a chip to fit in a space the size of a fingernail. The presence of a large number of transistors has enabled the classical computer to perform large calculations and complex procedures that help in solving day-to-day problems much faster.
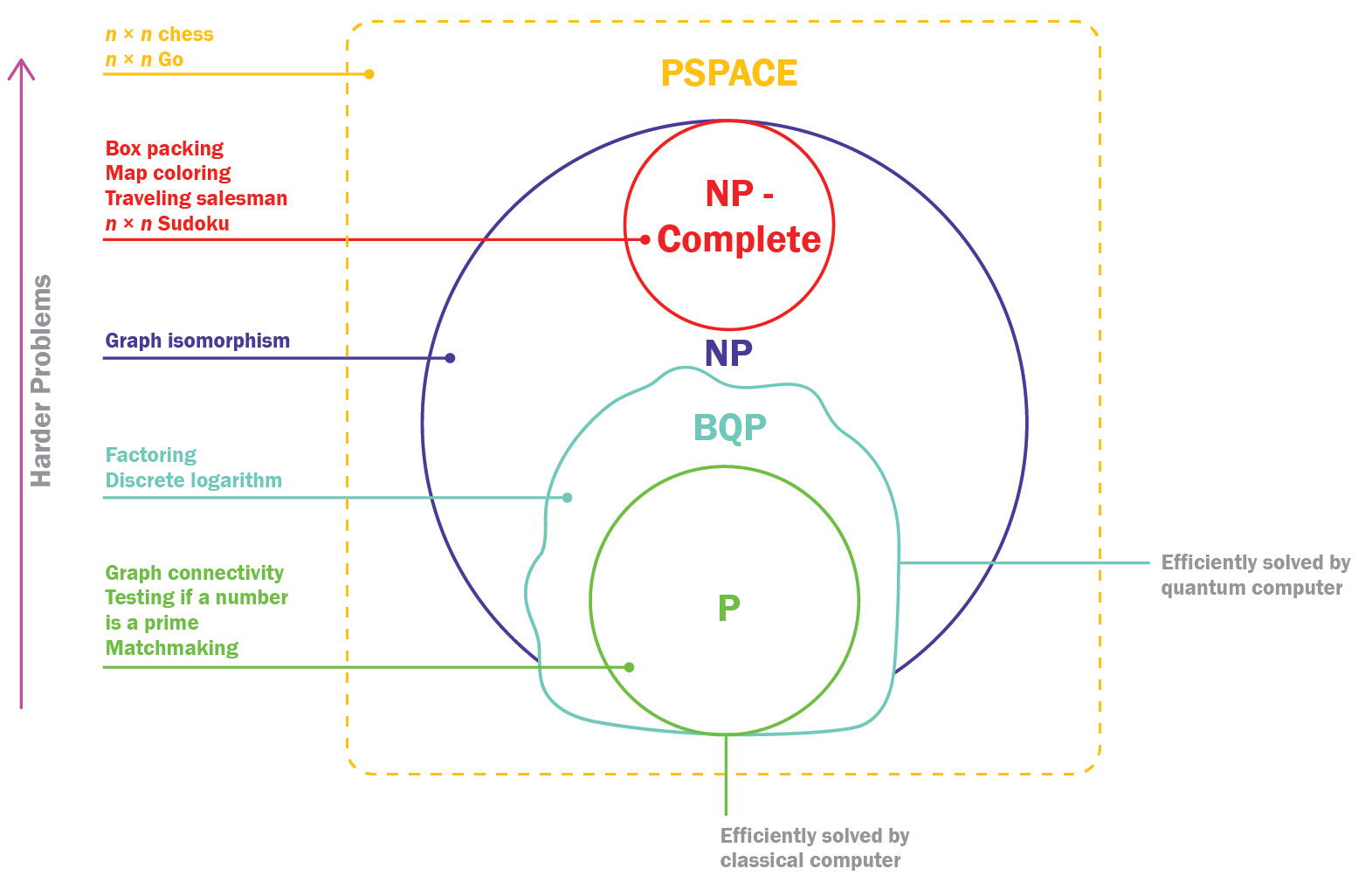
However, due to internal leakages and the miniaturization effect, classical gates (OR and AND gates) have been showcasing the quantum effect. Also, digital computers are traditionally unable to solve NP-hard problems (Figure 1.2). In layman’s language, NP-hard problems are measured by the amount of time it takes to solve a problem based on the complexity and number of variables. An example of this, as discussed previously, is how to choose the optimum route out of the 8,543,811,434,435,330 combinations determined for charging station locations in the San Francisco Bay Area. While it would take years for a classical computer to solve the aforementioned problem, ideally, quantum computers can solve it in 3 seconds.
Figure 1.2 – Classification of NP-hard problems based on level of complexity
To understand the limitations of classical computers in a better way, imagine that you have to pick a portfolio of 100 penny stocks with a limited budget, and let’s assume that the prices are discrete (for example, tick size on stock markets). Suppose you have to construct a portfolio in polynomial time (p = problems a computer can solve in a reasonable amount of time) and assume that it takes 100 steps (n = no. of inputs) to obtain an optimized portfolio or, in other words, n3 time. Theoretically, digital computers will solve the problem in three hours. This problem was easy to solve, and experts can easily verify the solution since we are dealing with stocks of the same class. Hence, we can confidently say that p-class problems are easy to check and solve. Now, the same problem but with a variation (a portfolio optimization of 100 stocks belonging to different risk classes in a limited time) will take around 300 quintillion years to solve, because although the solution is verifiable in a polynomial (n) timeframe, it is obtained in an exponential (NP) timeframe. This problem is classified as an NP problem. For an analogy, imagine a sudoku or tic-tac-toe problem: this is an NP problem for which it is difficult to obtain the solution (it takes exponential time), but easy to verify in polynomial time.
Following on from the preceding discussion, four types of NP problems that are deemed difficult to be solved by digital computers are as follows:
- Simulation: Computation simulation is modeling a natural world or physical system into a virtual scenario to understand its outcome and impact in advance. For instance, after the subprime crisis of 2008, financial institutions must run a stress test on their underlying assets and their crossholdings to predict the scenario in which the next financial crash could occur. According to one estimate, assessing the probability of a financial crash for a simple network of 20-30 institutions, having exposure in equity, derivatives, fixed income securities, and risk exposure to each other, would take 13.7 billion years, as calculated by a digital computer. This is the estimated time of running a simulation problem that is deterministic in nature and hints at solving a problem’s complexity in n steps in p time, which will not work using current digital technology and thus requires an advanced system to give a faster turnaround.
- Optimization: Optimization refers to improving the efficiency of an existing algorithm to reduce time complexity. Suppose you have to build a portfolio of 1,000 stocks belonging to 10 sectors. Your client, an international hedge fund, will have to generate several scenarios based on market conditions and thus look for an efficient frontier. These scenarios need to be updated in real time, adjusting themselves based on the risk tolerance limit defined for the portfolio. The classical computer may be able to solve the puzzle using parallel computing, but this might not be the most cost-effective and time-effective strategy. This problem underlies a need for an efficient computer to solve the puzzle in real time.
- Pattern recognition: The pattern recognition method uses underlying data to discover hidden patterns and trends using machine learning algorithms. However, recent advances in GPU and related technology have enabled programmers to meet with decent success in understanding and uncovering hidden patterns in the given data. In financial fraud, however, the complexity of human behavior makes it difficult for machine learning algorithms to understand the patterns. Theoretically, a computer able to comprehend data in real time can help decode the patterns of financial fraud more successfully.
- Cryptography: Providing a secure channel for customers to do transactions online in this e-connected world is a foremost priority for banks in the 21st century. All over the world, banks use Rivest, Shamir, and Adleman (RSA) technology based on linear factorization. The recent development of computing prowess hints that such encryption can be easily broken using quantum computers.
To summarize, it will suffice to say that with the limitations observed in current technology, it is time to explore new computing paradigms that can help solve the problems faced by the business fraternity at large and help the industry bring in innovations and creativity.



 Free Chapter
Free Chapter