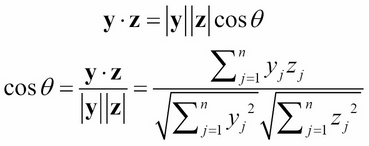If we think of each column y of the utility matrix as an n-dimensional vector, y = (y1, y2, ..., yn), then we can use the Euclidean dot product (inner product) formula to compute the cosine of the angle θ that the two vectors make at the origin:
This is called the cosine similarity
measure:
For example, if y = (2, 1, 3) and z = (1, 3, 2), then:
We can see that the cosine similarity measure has the six requisite properties for a similarity measure. If u and v are parallel, then s(y, z) = cos θ = cos 0 = 1. That would be the result in the case where y = (2, 1, 2) and z = (4, 2, 4). On the other hand, if y = (2, 0, 2) and z = (0, 4, 0), then y and z are perpendicular and s(y, z) = cos θ = cos 90º = 0.
We can interpret these extremes in terms of a utility matrix. If y = (2, 1, 2) and z = (4, 2, 4), then z = 2y. They are very similar in that all three of the users rated item z twice as high as item y. But in the second example of (2, 0, 2) and (0, 4, 0), we can detect no similarity...



 Free Chapter
Free Chapter